Blind Source Separation
Problem Definition
Blind Source Separation (BSS) problem arises in several different fields of study. In speech communication, a microphone in a room can simultaneously receive a mixture of several speech signals that need to be separated to render intelligible results. In biological studies, the sensors receive different electrical excitations where usually only one is of interest. In rotating machine vibration analysis for fault diagnosis, it is desired to separate the vibration due to faulty components. In each case, at least N sensors receive mixtures of N (statistically independent) sources. The objective is to restore (separate) the sources by observing only the mixtures. There are two classes of BSS algorithm, depending on the mixing process. In the scalar or instantaneous mixing case, the transfer function from each source to each sensor is a simple scalar. In the convolutive case, this transfer function is dynamic, with a nontrivial impulse response. In the vast majority of practical applications, the mixing is convolutive. Unfortunately, the BSS problem is far more difficult for the convolutive case than for the scalar case. Nevertheless, it is very important to develop a good solution for the instantaneous case, before extending it to the convolutive mixing problem. In this research, we are focusing on both of these cases, but with more emphasis on convolutive blind signal separation, since it has more practical significance.
Real Room Recordings Audio Samples
Matlab code implementing the blind source separation algorithm on data collected in a reverberant room is available on request by emailing Dr. Reilly: reillyj"AT"mcmaster"DOT"ca
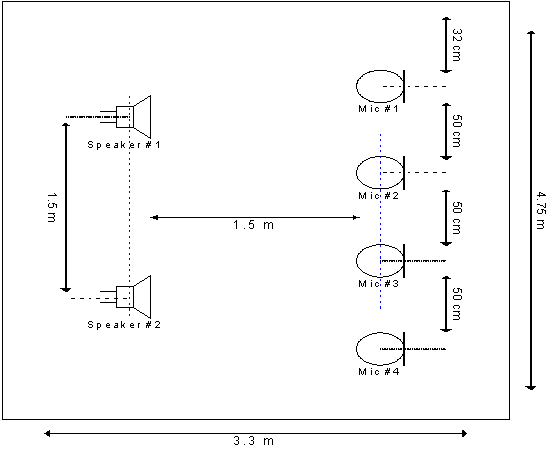
1. Results for recordings in an office room
Example 1: Speech & Speech
- Record Signal 1
- Record Signal 2
- Record Signal 3
- Record Signal 4
- Separated Output 1
- Separated Output 2
Example 2: Speech & Music
- Record Signal 1
- Record Signal 2
- Record Signal 3
- Record Signal 4
- Separated Output 1
- Separated Output 2
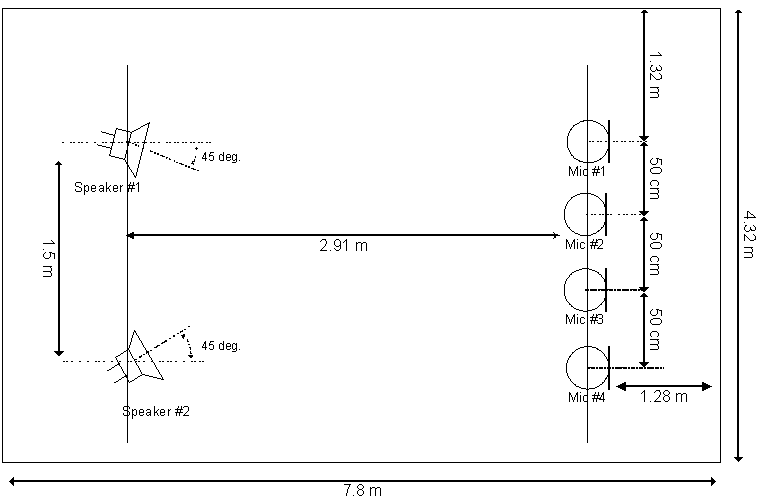
2. Results for recordings in a conference room
Example 1: Speech & Music
- Record Signal 1
- Record Signal 2
- Record Signal 3
- Record Signal 4
- Separated Output 1
- Separated Output 2
3. Results for recordings done by other researchers
For this example we used the real room recordings done by Lucas parra and Te-won Lee. The recordings have been downloaded from Lucas parra website.
Contributed By Te-Won Lee
Contributed By Lucas Parra
Research Update
Presented In ICASSP 2001
Abstract:
In this paper we present a new method for separating
non-stationary sources from their convolutive mixtures based on
approximate joint diagonalizing of the observed signals'
cross-spectral density matrices. Several blind source separation
(BSS) algorithms have been proposed which use approximate joint
diagonalization of a set of scalar matrices to estimate the
instantaneous mixing matrix. We extend the concept of approximate
joint diagonalization to estimate MIMO FIR channels. Based on this
estimate we then design a separating network which will recover
the original sources up to only a permutation and scaling
ambiguity for minimum phase channels. We eliminate the commonly
experienced problem of arbitrary scaling and permutation at each
frequency bin, by optimizing the cost function directly with
respect to the time-domain channel variables.
Submitted to ICA 2001
Abstract:
We consider the problem of blind sources separation of MIMO
convolutive mixtures for general case that number of sensors are
greater than or equal to the number of sources. We assume that
sources are non-stationary signals. The separation is performed in
frequency domain by joint minimization of the off diagonal
elements of observed signal's cross-spectral density matrices over
different epochs. We propose an efficient modified Newton
algorithm to minimize the cost function. We resolve the permutation
problem using a tree structured dyadic detection scheme. We find
and correct the wrong permutation at each frequency bin based on
cross frequency correlation between diagonal elements of the output
cross spectral matrices.