Blind Deconvolution and Source Separation using Particle Filtering with Application to the Dereverberation of Speech
Problem Definition
The reverberation of speech signals can cause significant degradation in the perceptual quality of speech at the ear of a person or for an audio recording device. Reverberation is the effect caused by multiple reflections of sound off the walls, floor and ceiling of the enclosure from the sound source to the microphone. Mathematically, this is the convolution of the actual speech with the long acoustic impulse response (AIR) of the room.
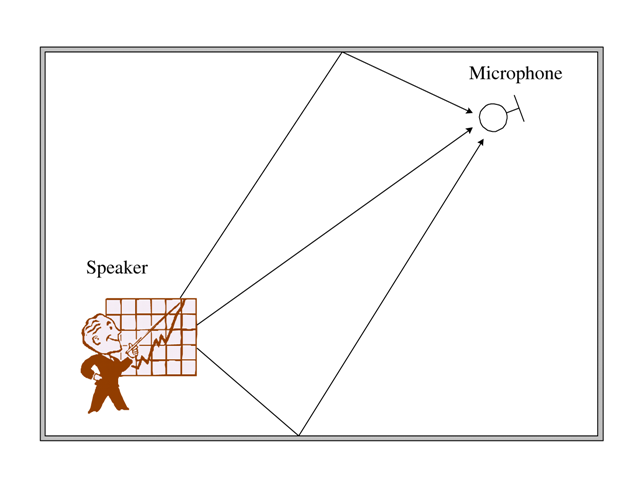
This reverberation is responsible for the annoying acoustical problem of the so-called barrel effect. Audio examples are presented here to demonstrate that the recorded signal in a reverberative room sounds far away, like at the bottom of a barrel.
Another problem that can cause difficulties in speech intelligibility and audio recording is known as the cocktail party phenomenon, which is caused when multiple speech sources are present simultaneously, along with other background noise such as moving fans and street traffic. The undesired speech sources and background noise act as interference on the desired speech signal.
Our goal is to reduce the detrimental effects of the barrel effect and cocktail party phenomenon on speech through the use of blind signal processing techniques. These techniques attempt to determine either the unknown input sources (blind deconvolution for single source, blind source separation for multiple sources) or the unknown channel (blind identification) using only the observed measurement signals.
Practical Applications
Although our primary focus is on audio applications, blind signal processing for deconvolution and source separation have application in a wide variety of fields, including:
- Hands-free telephony
- Digital hearing aids
- Music recording industry
- Teleconferencing
- Sonar and underwater acoustic telemetry
- Biomedical signal processing
- Geophysics
Algorithm Design
The nature of typical AIR for real rooms, as shown in the figure below, introduces three major design issues to be addressed when developing a blind signal processing algorithm for dereverberation:
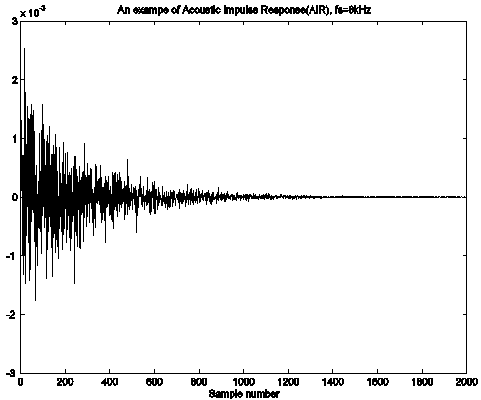
- Problem: Typical AIR can be as long as 250 ms (2000 samples), introducing a large computational cost. Algorithm: Decompose into smaller independent problems using filterbanks.
- Problem: AIR generally decay smoothly towards zero ("tailed") causing blind identification methods to be ill-conditioned. Algorithm: Directly estimate the source (blind deconvolution/source separation) by marginalizing out the channel to improve computational stability.
- Problem: The model with both an unknown source and channel is nonlinear, and in addition the statistics of the sources, channel and noise can be time-varying. Algorithm: Estimate the source using Sequential Monte Carlo methods (particle filters) to track the time-varying nature of the speech and acoustics, and handle nonlinear and non-Guassian models.
Filter Bank Implementation
To solve the computational tractability issue, we make use of a special subbanding structure referred to as complex filter banks or Generalized Discrete Fourier Transform filter banks. These filter banks inherently suppress aliasing in the subbands, (provided certain requirements on the analysis filters are met) and thus (approximately) eliminate the need for cross-filters between subbands. The result is that one large computationally intractable problem can be decomposed into many, much smaller, tractable pieces, allowing the overall problem to be solved. Download paper
Sequential Monte Carlo (Particle Filtering) Methods:
The ill-conditioned nature of the problem can be alleviated by using SMC methods to estimate the speech waveform directly, rather than blindly estimating or equalizing the channel. The posterior distribution of the speech given the measurements for a dynamic Bayesian state space model can be estimated and tracked efficiently using SMC methods. Results using particle filter expected shortly, while results using MCMC techniques are available in this paper: Blind Deconvolution using Bayesian Methods with Application to the Dereverberation of Speech
Algorithm Testing with Real Audio Data
An important aspect of the algorithm design is verifying the performance using collected data from a real reverberative room. It is anticipated that three sources of data will available for performance evaluation:
- Audio data in a reverberant room recorded with a large microphone array (Application: music recording, teleconferencing)
- Audio data in a reverberant room recorded with a head and torso model (KEMAR) as part of the McMaster Realistic Hearing-In-Noise Testing Environment System (R-HINT-E). Pictures below. The acoustic impulse response measurements collected from different angles, heights, and distances in a reverberative room are used to provide "soundscapes" for generating realistic signals for algorithm performance. (Application: hearing aids)
- Planned for summer 2004: Audio data in a moving car recorded with a microphone array (Application: hands-free telephony)