Computer Engineering 3SK3

Numerical Analysis

Academic year 2019-2020, term 2

Instructor: Xiaolin Wu, ITB-A315

Extension: 24190

Email: xwu@ece.mcmaster.ca

Lectures: 3 hours/week

Tutorial: 1 hour/week

TAs:

Chu, Xiaoxuan, chux7@mcmaster.ca; office hours: Monday, 1~4pm.  

ITB A204 Desk16.

Liang, Runchen, liangr19@mcmaster.ca; office hours: Tuesday 1~4 pm.

ITB A204, desk 5

Qian, Jingjing, qianj40@mcmaster.ca; office hours: Thursday 1~4 pm.

 ITB A203.

Luo, Fangzhou, luof1@mcmaster.ca; office hours: Wednesday 1~4 pm.

ITB A103

The course outline: 3sk3\CompEng_3SK3_outline_Winter2020.pdf

Lecture Notes: part1.pdf; part2.pdf; part3.pdf; part4.pdf; LinearProg.pdf; part5.pdf; Interpolation; part6.pdf; part7.pdf; 3sk3\interpolation.pdf

Tutorials: Tutorial_1 3SK3 2013.pdf, 3sk3\Tutorial_2.pdf, 3sk3\Tutorial_3.pdf

Textbook: “Numerical Methods for Engineers, Sixth edition”, by S. C. Chapra and R. P. Canale, McGraw Hill, 2010.

Course Objectives:

• Master basic techniques and algorithms for solving a wide range of numerical problems encountered in engineering.
• Understand the properties, strengths and limitations of common numerical methods.
• Acquire software skills for scientific and engineering computations.
• Learn to build suitable mathematical model(s) of a practical problem and choose the best possible tool(s) to solve it.

Main topics:

· Roots of Equations

· Linear Algebraic Equations

· Optimization Techniques

· Data Fitting

· Numerical Differentiation and Integration

· Differential Equations

Format: The course consists of class lecture sessions, tutorial session and a laboratory component. The lab component of the course consists of two small projects that students can do on their own time schedule.

Assessment scheme:

Tests: 20%

Final: 60%

Projects: 20%

Course Project (TBA)

*************************************************************

OLD COURSE MATERIALS (for references only):

Sample midterm exam Midterm11.pdf

Answers to midterms 1 and 2: Answers

Sample questions for the final exam. Sample exam questions

Marks of Assignments 1 and 2 A1A2 Marks.pdf

_____________________________________________________________________________

Assignment 1 (Due January 17, 2014):

Prove the following two definitions of machine precision are equivalent.

1. Machine precision is the maximum relative error.

2. Machine precision is the smallest number e such that fl(1+e)>1.

What is the machine precision for IEEE 64-bit floating point format?

_________________________________________________________________________________

Assignment 2 (Due January 31, 2014)

Prove function has a unique root in interval [0,1]. If the bisection search method

is used to find the root, how many iterations are required to ensure that the error is below ?

How many iterations does the Newton-Raphson method require to achieve the same precision?

How many iterations does the False-point method require to achieve the same precision?

_________________________________________________________________________________

Sample questions: 3sk3\Sample Q1.pdf, 3sk3\Sample Q2.pdf, 3sk3\Sample Q3.pdf, 3sk3\Sample Q4.pdf,

More exercise questions are in

Textbook: “Numerical Methods for Engineers, Sixth edition”, by S. C. Chapra and R. P. Canale, McGraw Hill, 2010.

Q13.2 (ed.5) (answer x = 0.91692)

Q13.3 (ed.5) (the 3^rd estimate x* = 0.9443)

Q13.5 (ed.5) (the result after three iterations is x*=1.047716)

Q13.11 (ed.5) (x = -0.5867)

Q14.2 (ed.5) ()

Q14.3 (ed.5)

answer for (b) is

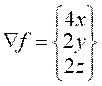
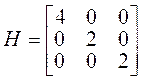
Q14.6 (ed.5) (one iteration suffices to converge)

Yes more sample questions:

17.4 ed.5 (17.3 ed.6), 17.9 ed.5 (17.8 ed.6), 17.13 ed.5 (17.12 ed.6), 17.14 ed.5, 17.16 ed.5 (17.18 ed.6)

18.5 ed.5 (18.6 ed.6), 18.7 ed.5 (18.7 ed.6)

21.1, 21.2 (both ed.5 and ed.6)

22.1, 22.3 (both ed.5 and ed.6)

23.1, 23.3, 23.4 (both ed.5 and ed.6)

25.2 ed.5